先月、GIMPSによって発見された５１番目のメルセンヌ素数。５１番目に発見されただけで下から５１番目かどうかは未定。
これが現在までに発見された最大素数で１０進法での桁は２４８６万２０４８桁だとか。これって２０進法だと何桁なんだろ。計算したくてもこの桁数だと普通のコンピュータでは無理。
そういえばメルセンヌ素数が無数あるのかどうかは未だ証明されていない。素数自体が無数に存在すること自体はだいぶ前に証明されているし、その式自体の論理自体は誰でも分かる様なものなのに。不思議。
先週末日本語の授業を受け持つこととなった。
日本語を教えるのは初めてのことだったのでスライドを準備。ひらがなとカタカナの書き方を効率良く教えようとmedia9を使って動画を取り込むこととした。
アニメーション自体はAfter Effectsを利用。
コードは近い内に公開予定。PDFに取り込んだ画像に一部ミスがあったので後程修正した。
スライドはこちら。
最近このテーマの問題について聞かれることが多かったけど、関連して昨日は円周率の話。中学生なので円周率が3.14…ということと、それがつまり３から４の間ということについて。
確かガウスが何か言っていたなぁとか考えていたら東大で関連した入試問題があったことに気づいた。
円周率が3.05より大きいことを証明せよ
これ自体は三角関数と余弦定理を知っていれば比較的簡単に解けると思う。で今回のテーマにピッタリ。日本では高校数学では電卓は使わないと思うのでその場合正８角形か正１２角形で解くのかな。電卓が使えるこちらではもっと細かくして円周率により近い証明が出来る。
これってこちらの高校生も解けるのかな？余弦定理はこちらの私立学校であれば中三レベルでもカバーしているけど余弦定理を必要とする論理に辿り着くかどうかが分からない。
面白い問題だし今後のために遊び心でこんなものを作ってみた。
TeXコードはこちら。ベクター素材が必要な方は連絡ください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
\begin{center} \definecolor{orange}{RGB}{191,87,0} \Huge \def\arraystretch{1.5} \begin{tabular}{|C{3cm}|C{3cm}|C{3cm}|C{3cm}|C{3cm}|C{3cm}|} \hline \textcolor{orange}{\(\theta\)} & \includegraphics[width=1cm]{00}\textcolor{orange}{\(^\circ\)} & \includegraphics[width=1cm]{01} \includegraphics[width=1cm]{10} \textcolor{orange}{\(^\circ\)} & \includegraphics[width=1cm]{02} \includegraphics[width=1cm]{05} \textcolor{orange}{\(^\circ\)} & \includegraphics[width=1cm]{03} \includegraphics[width=1cm]{00} \textcolor{orange}{\(^\circ\)} & \includegraphics[width=1cm]{04} \includegraphics[width=1cm]{10} \textcolor{orange}{\(^\circ\)} \\ \hline \textcolor{orange}{sin \(\theta\)} & \includegraphics[width=1cm]{h00} & \textcolor{orange}{\(\frac{\includegraphics[width=.7cm]{h01}}{\includegraphics[width=.7cm]{h02}}\)}& \textcolor{orange}{\(\frac{\sqrt{\includegraphics[width=.7cm]{h02}}}{\includegraphics[width=.7cm]{h02}}\)}& \textcolor{orange}{\(\frac{\sqrt{\includegraphics[width=.7cm]{h03}}}{\includegraphics[width=.7cm]{h02}}\)}& \includegraphics[width=1cm]{h01} \\\hline \textcolor{orange}{cos \(\theta\)} & \includegraphics[width=1cm]{h01} & \textcolor{orange}{\(\frac{\sqrt{\includegraphics[width=.7cm]{h03}}}{\includegraphics[width=.7cm]{h02}}\)}& \textcolor{orange}{\(\frac{\sqrt{\includegraphics[width=.7cm]{h02}}}{\includegraphics[width=.7cm]{h02}}\)}& \textcolor{orange}{\(\frac{\includegraphics[width=.7cm]{h01}}{\includegraphics[width=.7cm]{h02}}\)}& \includegraphics[width=1cm]{h00} \\\hline \textcolor{orange}{tan \(\theta\)} & \includegraphics[width=1cm]{h00} & \textcolor{orange}{\(\frac{\includegraphics[width=.7cm]{h01}}{\sqrt{\includegraphics[width=.7cm]{h03}}}\)}& \includegraphics[width=1cm]{h01}& \textcolor{orange}{\(\sqrt{\includegraphics[width=1cm]{h03}}\)}& \textcolor{orange}{\bf ---}\\\hline \end{tabular} \end{center} \huge \textquestiondown Jasche \(\pi > 3.05\) (\(\pi \approx 3.141592\))? |
恩師の一人が亡くなった。
院生の頃、色んな面でお世話になった人。分野が違うので博論のコミッティーには入らなかったけどあの頃、アカデミックな面に限らず色んなことを教わった。
あの時のランチは生涯忘れることはないだろうし、引退パーティーやPAAでご一緒出来たことも光栄。
その時が来たと言えばそうなんだろうけど、ただただ悲しい。
Ch’ab’ej chik, ri wajtij Parker.
GISはマップ作りのみに活用している。集落毎の距離を算出して回帰分析に独立変数として取り入れたことも以前はあったけれど、距離が必ずしもアクセスし易さと一致しないことからあまりウェートを置いていない。意味が無い訳では決してないんだけど、計算に労力を使う位なら他にやるべきことは沢山ある。モデルもよりフィットする訳ではないし。
グアテマラの場合今までは国連関係や農牧食糧省から購入したシェイプ・ファイルを使ってきたけど、これらのデータの難点は市レベルまでしかないこと。センサスには集落レベルまで考慮されているのでデータはあるかもとは思っていたけど、最後に調査されたのが２００２年なので当時のGPSの普及状況を考えれば位置情報を取っていなくても不思議ではなく、はっきりしないまま市レベルのデータ（境界線）を使ってきた。
久方振りにGISを使うこととなったのでネット検索してみたらSEGEPLANがデータを持っていた。
早速ダウンロードして試してみた。最近GISはArcViewではなく、オープンソースのQGISを使っている。パソコンへのインストールの制限もないのでどこでも使えるから。使途も限られているのでこれで十分。
カンテルで見た場合、場所はあっている。Google Earthに読み込んでみた。
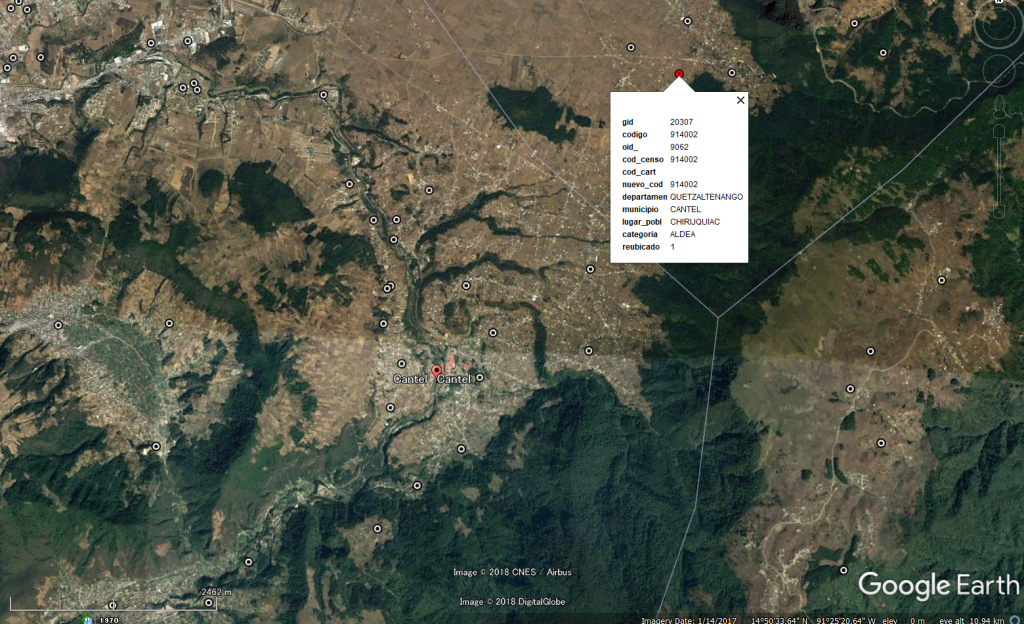
カンテルと検索して矢印が出るのはカンテルの象徴とも言える繊維工場、ファブリカがある場所。クリックした所はチリフキアック(Chirijquiac)集落。Quiacはキチェ語でk’iyaq、ノミという意味。Chirijが後ろという意味なので「ノミの後ろ」という意味。この名前はある伝説に由来して近辺にはチョキアック、ショルキアックというノミとの位置関係に由来した名前の集落が他に２つある。
今回、新たにシェイプ・ファイルを入手出来たことに加えてSEGEPLANは２００２年センサスのアグレゲート・データも作成していたので、これを機会にデータの加工もこれまでのStataではなくRでやろうと思う。速度的にはSTATAの方が断然優れているけれど一つの環境で全ての作業が出来るメリットは大きいし、何よりRは大抵のパソコンに入れることが出来る。
