国際デジタル絵本学会の協力の下，ポポル・ブフ第一章の絵本動画を作ってみた。日・西・キチェ語の三つのバージョンを作る予定だけと取り合えずキチェ語バージョン。
Popolは共同体という意味だけどこれはペタテと呼ばれるマット(pop)に由来する。編む様子が人々の交流を表すから共同体となった。ある意味中島みゆきの「糸」に通ずるところがあると思う。
動画作成にあたり色んなバージョンのポポル・ブフを日本語，キチェ語（JICAが協力したものも１０年振りに読んだ。），英語，スペイン語で読んだけど一番クオリティが高いのはサム・コロップのスペイン語版かなと感じた。有名なレシーノスのものはサム・コロップが指摘するように詳細が抜けていると思う。キチェ語圏文化に対する理解が高くないとその辺は難しい。実際，今回読み直して如何にこの本がキチェ語圏の文化に密接に関わっているか如実に感じたし。
レシーノス版をベースとした林屋氏の日本語版は素晴らしいけど，本当にこの本を理解するにはサム・コロップ版を訳す必要があるのかな。
不思議な感じがするけど今までLaTeXでページ番号を用いない文書を作ったことがないらしい。今日その必要性に駆られて調べることとなったから。
方法は単純。この一行を入れるのみ。
|
1 |
\pagenumbering{gobble} |
今週末のスピーチの原稿のドラフト。
LaTeXで文章を右寄せにする方法を忘れてた。以前一度だけやった記憶があるけど、普段英語で文章を書くので殆どその必要がない。でやり方。
|
1 2 3 |
\begin{flushright} Ub'antajik tzij \end{flushright} |
こんな風に書けた。
最近このテーマの問題について聞かれることが多かったけど、関連して昨日は円周率の話。中学生なので円周率が3.14…ということと、それがつまり３から４の間ということについて。
確かガウスが何か言っていたなぁとか考えていたら東大で関連した入試問題があったことに気づいた。
円周率が3.05より大きいことを証明せよ
これ自体は三角関数と余弦定理を知っていれば比較的簡単に解けると思う。で今回のテーマにピッタリ。日本では高校数学では電卓は使わないと思うのでその場合正８角形か正１２角形で解くのかな。電卓が使えるこちらではもっと細かくして円周率により近い証明が出来る。
これってこちらの高校生も解けるのかな？余弦定理はこちらの私立学校であれば中三レベルでもカバーしているけど余弦定理を必要とする論理に辿り着くかどうかが分からない。
面白い問題だし今後のために遊び心でこんなものを作ってみた。
TeXコードはこちら。ベクター素材が必要な方は連絡ください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
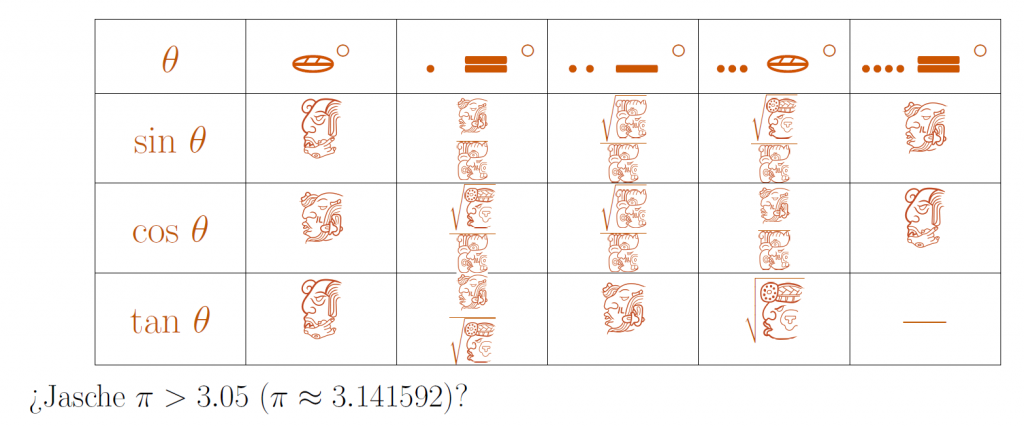
\begin{center} \definecolor{orange}{RGB}{191,87,0} \Huge \def\arraystretch{1.5} \begin{tabular}{|C{3cm}|C{3cm}|C{3cm}|C{3cm}|C{3cm}|C{3cm}|} \hline \textcolor{orange}{\(\theta\)} & \includegraphics[width=1cm]{00}\textcolor{orange}{\(^\circ\)} & \includegraphics[width=1cm]{01} \includegraphics[width=1cm]{10} \textcolor{orange}{\(^\circ\)} & \includegraphics[width=1cm]{02} \includegraphics[width=1cm]{05} \textcolor{orange}{\(^\circ\)} & \includegraphics[width=1cm]{03} \includegraphics[width=1cm]{00} \textcolor{orange}{\(^\circ\)} & \includegraphics[width=1cm]{04} \includegraphics[width=1cm]{10} \textcolor{orange}{\(^\circ\)} \\ \hline \textcolor{orange}{sin \(\theta\)} & \includegraphics[width=1cm]{h00} & \textcolor{orange}{\(\frac{\includegraphics[width=.7cm]{h01}}{\includegraphics[width=.7cm]{h02}}\)}& \textcolor{orange}{\(\frac{\sqrt{\includegraphics[width=.7cm]{h02}}}{\includegraphics[width=.7cm]{h02}}\)}& \textcolor{orange}{\(\frac{\sqrt{\includegraphics[width=.7cm]{h03}}}{\includegraphics[width=.7cm]{h02}}\)}& \includegraphics[width=1cm]{h01} \\\hline \textcolor{orange}{cos \(\theta\)} & \includegraphics[width=1cm]{h01} & \textcolor{orange}{\(\frac{\sqrt{\includegraphics[width=.7cm]{h03}}}{\includegraphics[width=.7cm]{h02}}\)}& \textcolor{orange}{\(\frac{\sqrt{\includegraphics[width=.7cm]{h02}}}{\includegraphics[width=.7cm]{h02}}\)}& \textcolor{orange}{\(\frac{\includegraphics[width=.7cm]{h01}}{\includegraphics[width=.7cm]{h02}}\)}& \includegraphics[width=1cm]{h00} \\\hline \textcolor{orange}{tan \(\theta\)} & \includegraphics[width=1cm]{h00} & \textcolor{orange}{\(\frac{\includegraphics[width=.7cm]{h01}}{\sqrt{\includegraphics[width=.7cm]{h03}}}\)}& \includegraphics[width=1cm]{h01}& \textcolor{orange}{\(\sqrt{\includegraphics[width=1cm]{h03}}\)}& \textcolor{orange}{\bf ---}\\\hline \end{tabular} \end{center} \huge \textquestiondown Jasche \(\pi > 3.05\) (\(\pi \approx 3.141592\))? |
恩師が亡くなって少し時間が経った。今は悲しいと気持ちより不安の方が大きい。彼に限らず最近は何人かの知り合いが亡くなった。自分の年齢が上がるにつれ結果的に付き合う人の年齢層も上がるので死亡率が高まっているのかもしれない。そもそも付き合いのある人達が年上のことが多い。正確には同年代があまりいなく、年上か大学生位の年代が多いのかもしれない。
まぁそれは余談で年上の人が亡くなると不安になる。今まで頼ってきた人が居なくなり独り立ちしろと言われているようで。もちろんそういう年齢ではあるけれど、それでも何かあった時に頼れる人が少しずつ少なくなっていくというのは不安でもある。恩師の様に色んな相談にのってもらえた人を亡くした時は特に。今後はどう生きようかとか色々考える。
最近見た動画。スピーチの内容も素晴らしいし、テキサスのアクセントが懐かしい。
